heap 이란?
최대 heap 이란 두 가지 조건을 만족하는 이진트리이다.
- complete binary tree
- parents node >= child node (최소 heap 은 parents node <= child node)
최대 heap 이면 전체 데이터 중 루트 노드가 가장 큰 데이터가 된다.
(예)
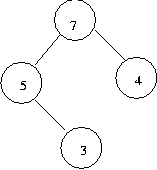
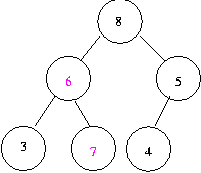
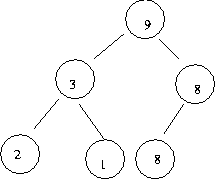
heap 이 아님
(complete binary tree 가 아님)
heap 이 아님
(parnents >= child node 가 조건에 위배)
heap
- complete binary tree
- parents node >= child node (최소 heap 은 parents node <= child node)
(예)
 |
 |
 |
| heap 이 아님 (complete binary tree 가 아님) |
heap 이 아님 (parnents >= child node 가 조건에 위배) |
heap |
heap 구조는 언제 사용하는가?
수시로 데이터가 삽입되는 구조에서 삽입된 데이터 중 가장 큰 데이터(혹은 작은 데이터)를 가져오고자 하는 경우
예를 들어, 100 만건의 데이터가 있는 경우 이 중 가장 큰 데이터를 가져오기 위해서는 평균 50 만 번의 비교가 일어날 것이다.
heap 구조로 이를 처리한다면 100 만건의 데이터가 있을 때 최악의 경우도 약 20 번, 평균 10 번 정도의 비교로 일을 끝낼 수 있다. (수시로 데이터가 삽입이 되므로 미리 소트해서 사용할 수는 없다)
이런 삽입,삭제가 무수히 발생한다면 실행속도는 비교도 할 수 만큼의 차이를 보일 것이다. 이것이 heap 의 위력이다.
예를 들어, 100 만건의 데이터가 있는 경우 이 중 가장 큰 데이터를 가져오기 위해서는 평균 50 만 번의 비교가 일어날 것이다.
heap 구조로 이를 처리한다면 100 만건의 데이터가 있을 때 최악의 경우도 약 20 번, 평균 10 번 정도의 비교로 일을 끝낼 수 있다. (수시로 데이터가 삽입이 되므로 미리 소트해서 사용할 수는 없다)
이런 삽입,삭제가 무수히 발생한다면 실행속도는 비교도 할 수 만큼의 차이를 보일 것이다. 이것이 heap 의 위력이다.
heap 의 구현
heap 구조는 complete binary tree 이므로 , 배열로 표현하는게 유리하다.
- i 번째 노드의 아버지노드 : i/2
- i 번째 노드의 왼쪽 아들: 2*i
- i 번째 노드의 오른쪽 아들: 2*i + 1
heap insert____
추가 데이터와 추가 노드의 조상노드(아버지,할아버지,증조 할아버지....)와 차례로 비교하면서 조상노드가 작으면 내리고 아니면 내린 노드의 위치에 데이터를 위치시키는 방법.
예를 들면,
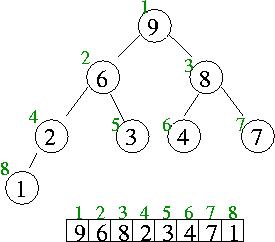
초기 heap 의 상태가 데이터 수 n 은 8 이고 왼쪽과 같은 경우 , 이 heap 에 데이터 item 7 을 추가하는 경우를 생각해보자.
먼저 데이터 수 n 은 8 에서 하나 증가해 9 가되고, 이 값을 임시변수 i 가 갖는다.
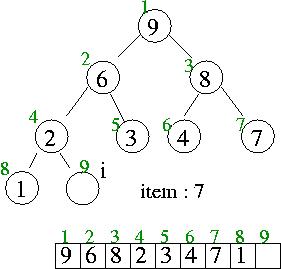
i
item
heap[i/2]
9
7
2
item > heap[i/2] 이므로 heap[i/2] 는 i 위치로 i 는 parents 노드로
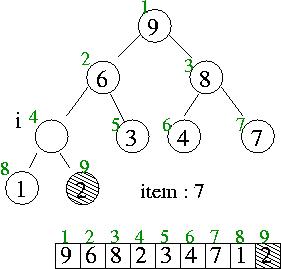
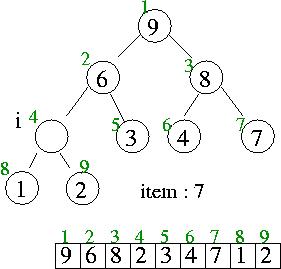
i
item
heap[i/2]
4
7
6
item > heap[i/2] 이므로 heap[i/2] 는 i 위치로 i 는 parents 노드로
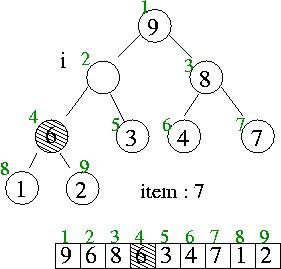
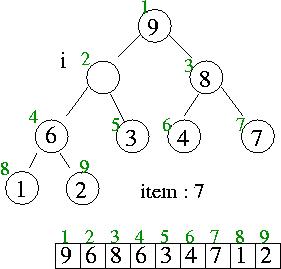
i
item
heap[i/2]
2
7
9
item <= heap[i/2] 이므로 item 을 i 번째 위치 끝.....
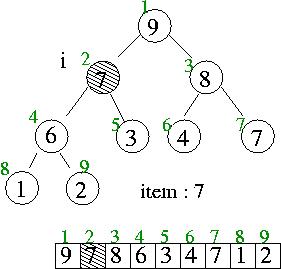
heap delete...
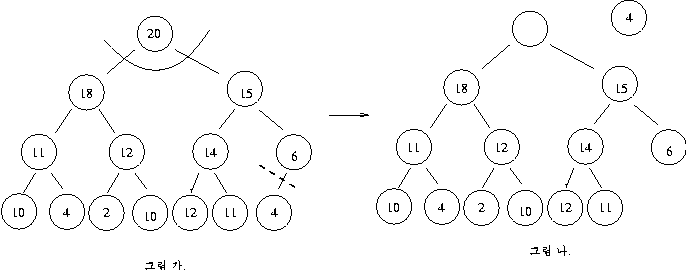
루트노드(그림에서는 20)를 자른 후 다음을 위하여 재차 heap 을 만들어야 한다.
complete binary tree 가 되어야 하므로 마지막 노드(그림에서 3)를 자른 후 , 세 값(4,18,15)을 비교후 가장 큰 데이터가 올라오는 동작이 반복되다 자른 데이터가 가장 크거나 같으면 위치시키는 과정이다.
- i 번째 노드의 아버지노드 : i/2
- i 번째 노드의 왼쪽 아들: 2*i
- i 번째 노드의 오른쪽 아들: 2*i + 1
heap insert____
추가 데이터와 추가 노드의 조상노드(아버지,할아버지,증조 할아버지....)와 차례로 비교하면서 조상노드가 작으면 내리고 아니면 내린 노드의 위치에 데이터를 위치시키는 방법.
예를 들면,
|
|
초기 heap 의 상태가 데이터 수 n 은 8 이고 왼쪽과 같은 경우 , 이 heap 에 데이터 item 7 을 추가하는 경우를 생각해보자. 먼저 데이터 수 n 은 8 에서 하나 증가해 9 가되고, 이 값을 임시변수 i 가 갖는다.
| |||||||
|
|
item > heap[i/2] 이므로 heap[i/2] 는 i 위치로 i 는 parents 노드로 |
| ||||||
|
|
item > heap[i/2] 이므로 heap[i/2] 는 i 위치로 i 는 parents 노드로
|
| ||||||
|
|
item <= heap[i/2] 이므로 item 을 i 번째 위치 끝.....
|
 |
heap delete...

루트노드(그림에서는 20)를 자른 후 다음을 위하여 재차 heap 을 만들어야 한다.
complete binary tree 가 되어야 하므로 마지막 노드(그림에서 3)를 자른 후 , 세 값(4,18,15)을 비교후 가장 큰 데이터가 올라오는 동작이 반복되다 자른 데이터가 가장 크거나 같으면 위치시키는 과정이다.
우선 순위 큐란?
queue 구조는 먼저 들어간 데이터가 먼저 나오는 구조이지만 , heap 구조는 들어간 순서에 관계없이 최대 혹은 최소값이 먼저 나오므로 이러한 구조를 우선순위 큐(priority queue)라 한다.
queue 구조는 먼저 들어간 데이터가 먼저 나오는 구조이지만 , heap 구조는 들어간 순서에 관계없이 최대 혹은 최소값이 먼저 나오므로 이러한 구조를 우선순위 큐(priority queue)라 한다.
'MISCELLANEOUSNESS' 카테고리의 다른 글
| [SWT] SWT 개발 환경 설정하기 (0) | 2007.09.15 |
|---|---|
| [UNIX/LINUX] FTP 기본 명령어 (0) | 2007.09.15 |
| [UNIX] UNIX 기본 명령어 (0) | 2007.09.15 |